Round Square Combinations are Surprising
All four of these solids are Round Squares. I thought I had a general rule for calculating the combinations when I found the first two but then I found another and another. Is there a general formula for all the possible combinations. What are the parameters? Numerically there could be 6 but I do not think geometrically 6 are possible. This gets more confusing for Round Triangles or Square Triangles.
Cylinder is the obvious round square.
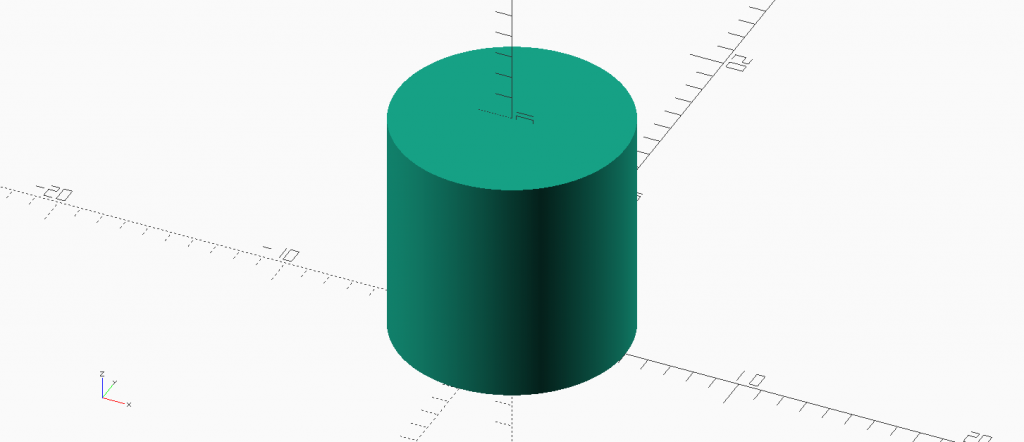
Cones are round triangle. Two triangles for a square. Two cones form a round square.
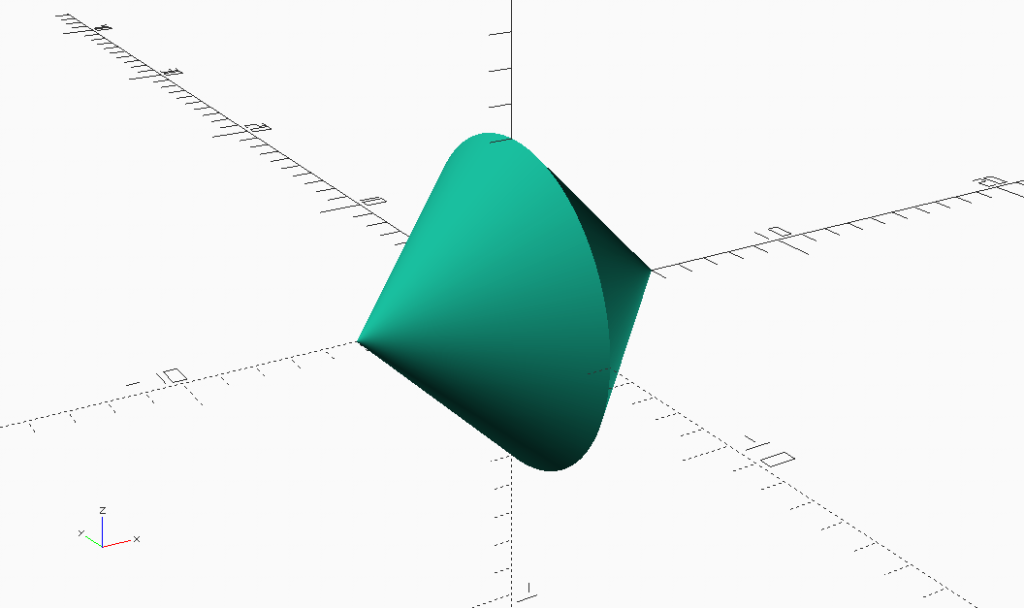
Combinations of 3D shapes are either unions or intersections. The intersection of a cylinder and a wedge makes a Round Square Triangle. The union of two half height Round Square Triangles form a Round Square.
Intersection of two cylinders rotates 90 degrees from each other leaves a square and two rounded sides for the Fourth Round Square.
I found the first two using pencil and paper. The third with FreeCAD thinking in a subtractive then additive fashion. The fourth I found using OpenSCAD. The different approaches enabled finding the alternatives. I would not have found the fourth type using pencil and paper, the CAD software showed me what I described.
How would you go about finding a proof for a general formula?
Benoit Mandelbrot passed away 1924-2010
Benoit Mandelbrot, the mathematician who discovered fractals has passed away at age 85. I owe his genius for some fundamental concepts that make the Predictive Innovation® possible.
Is P vs NP solved?
Vinay Deolalikar from HP Labs claims he may have solved the P vs NP problem proving that P ≠ NP. It’s literally a million dollar problem. Millennium Prize is offering $1,000,000 for the solution. This is very important for a range of problems including: cryptography, logistics, biology, mathematics, and innovation.
If P ≠ NP is true, it would allow a person to formally show that a problem cannot be solved efficiently, so attention could be focused on partial solutions or solutions to other problems. Or as I say in my talks about applying information theory to science, “Being able to prove something is impossible helps you focus on the things that might be possible.”
The other implication is that some problems can be proven to be harder to solve than to test that the solution is true. This is very important to cryptography. If P = NP then many of the encryption methods would be easy to break and would need to be changed.
Hard to solve, easy to check also directly relates to innovation. I run into this all the time. A company has what they believe is an impossible problem. After we apply the Predictive Innovation® and find the solution they think the solution was obvious. It was far easier to check the answer than it was to solve the problem. In fact it was so easy to check the answer they didn’t understand why it was so hard to find in the first place. I would not be surprised if P ≠ NP was proved.
Predictive Innovation Training
Predictive Innovation: Core Skills Book
RoundSquareTriangle.com