Round Square Combinations are Surprising
All four of these solids are Round Squares. I thought I had a general rule for calculating the combinations when I found the first two but then I found another and another. Is there a general formula for all the possible combinations. What are the parameters? Numerically there could be 6 but I do not think geometrically 6 are possible. This gets more confusing for Round Triangles or Square Triangles.
Cylinder is the obvious round square.
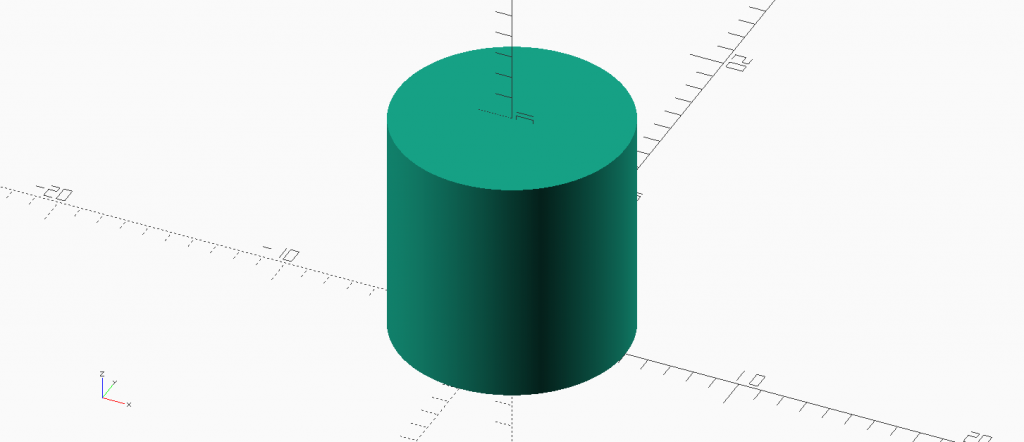
Cones are round triangle. Two triangles for a square. Two cones form a round square.
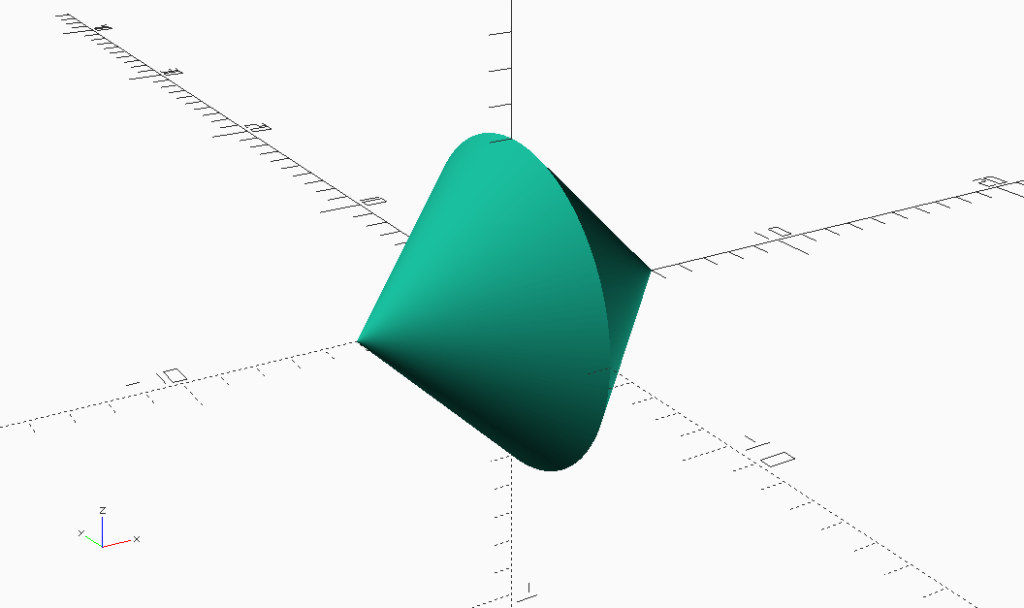
Combinations of 3D shapes are either unions or intersections. The intersection of a cylinder and a wedge makes a Round Square Triangle. The union of two half height Round Square Triangles form a Round Square.
Intersection of two cylinders rotates 90 degrees from each other leaves a square and two rounded sides for the Fourth Round Square.
I found the first two using pencil and paper. The third with FreeCAD thinking in a subtractive then additive fashion. The fourth I found using OpenSCAD. The different approaches enabled finding the alternatives. I would not have found the fourth type using pencil and paper, the CAD software showed me what I described.
How would you go about finding a proof for a general formula?
Mathematics Behind Predictive Innovation
FutureMaps created using the Predictive Innovation Method are truly maps of the innovation space. Each innovation has a specific address and any desired set of innovations can be located by using the proper combination of parameters.
The Predictive Innovation Method constructs an n dimensional taxonomy (hypercube) to describe the innovation space. This is in essence a fractal model. By increasing dimensions, greater resolution can be achieved at predictable levels. This improves upon hierarchical taxonomies by allowing for multiple classifications and sparsely populated hypercubes.
Similar approaches have been used in computer graphics to highly accurately represent natural systems. This shares some similarity to the work of Stephen Wolfram on cellular automata models.
Extra Credit
If all that was a bunch of geeky gobly gook to you then you can at least enjoy the pretty picture and this fun song by Jonathan Coulton’s called “Mandelbrot Set”. You might want to visit his website. He has some great music and he has done some cool things with Creative Commons.
Mathematics Behind Predictive Innovation®
FutureMaps created using the Predictive Innovation® are truly maps of the innovation space. Each innovation has a specific address and any desired set of innovations can be located by using the proper combination of parameters.
The Predictive Innovation® constructs an n dimensional taxonomy (hypercube) to describe the innovation space. This is in essence a fractal model. By increasing dimensions, greater resolution can be achieved at predictable levels. This improves upon hierarchical taxonomies by allowing for multiple classifications and sparsely populated hypercubes.
Similar approaches have been used in computer graphics to highly accurately represent natural systems. This shares some similarity to the work of Stephen Wolfram on cellular automata models.
Extra Credit
If all that was a bunch of geeky gobly gook to you then you can at least enjoy the pretty picture and this fun song by Jonathan Coulton’s called “Mandelbrot Set”. You might want to visit his website. He has some great music and he has done some cool things with Creative Commons.
Predictive Innovation Training
Predictive Innovation: Core Skills Book
RoundSquareTriangle.com