Round Square Combinations are Surprising
All four of these solids are Round Squares. I thought I had a general rule for calculating the combinations when I found the first two but then I found another and another. Is there a general formula for all the possible combinations. What are the parameters? Numerically there could be 6 but I do not think geometrically 6 are possible. This gets more confusing for Round Triangles or Square Triangles.
Cylinder is the obvious round square.
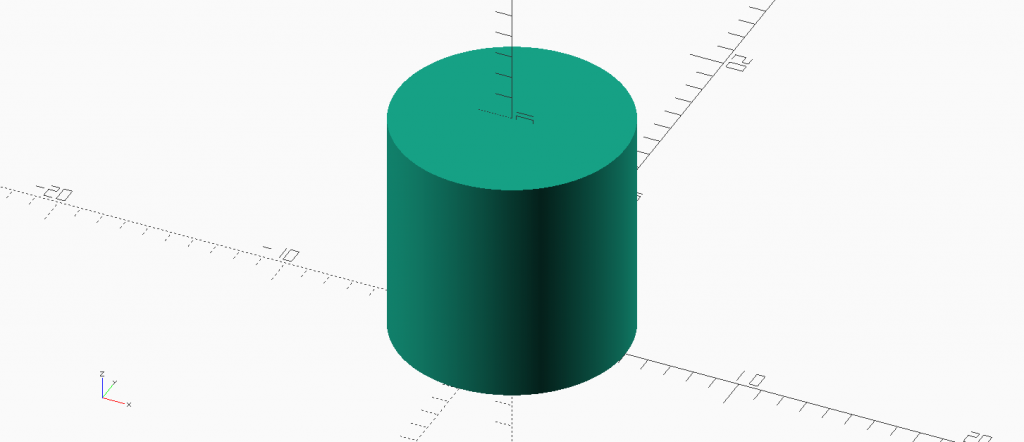
Cones are round triangle. Two triangles for a square. Two cones form a round square.
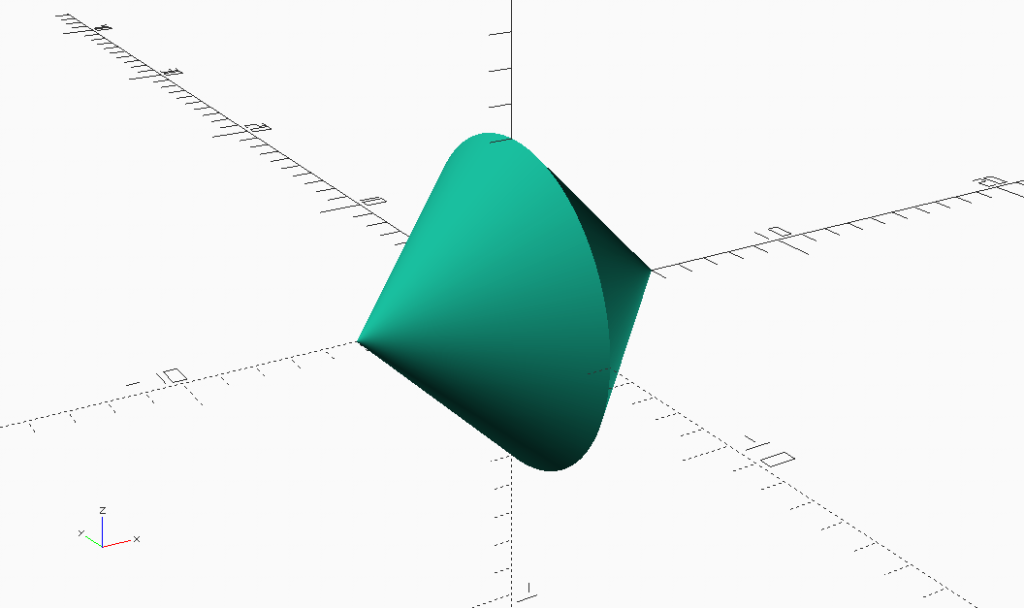
Combinations of 3D shapes are either unions or intersections. The intersection of a cylinder and a wedge makes a Round Square Triangle. The union of two half height Round Square Triangles form a Round Square.

Intersection of two cylinders rotates 90 degrees from each other leaves a square and two rounded sides for the Fourth Round Square.

I found the first two using pencil and paper. The third with FreeCAD thinking in a subtractive then additive fashion. The fourth I found using OpenSCAD. The different approaches enabled finding the alternatives. I would not have found the fourth type using pencil and paper, the CAD software showed me what I described.
How would you go about finding a proof for a general formula?


 Predictive Innovation Training
Predictive Innovation Training Predictive Innovation: Core Skills Book
Predictive Innovation: Core Skills Book RoundSquareTriangle.com
RoundSquareTriangle.com